How to Check Well-Formatted Brackets in Expressions | Coding Guide

Define your Algorithm and Steps to implement

First, we need one Stack (LIFO — Last In First Out), where we can push and pop the characters one by one.

How to Create a Stack in Java?

we must import java.util.stack package and use the Stack() constructor of this class

Stack<E> stack = new Stack<E>();

We will loop the Input expression and read each character inside a for loop.

In the initial stage, the stack will be empty and we will loop a string containing expressions.

Then we will check, if it is starting bracket like ‘[’,’{’,’(’ — any of them, then push it into the stack.

If we have a closing bracket, then we will compare it with the stack using the pop() method. If the current character matches with the same kind then we will continue and check the next remaining characters; otherwise, break it and print output as “Not Paired”.

I heard that Image says thousands of words.

Let me add one image to tell you the above steps with some visualization.

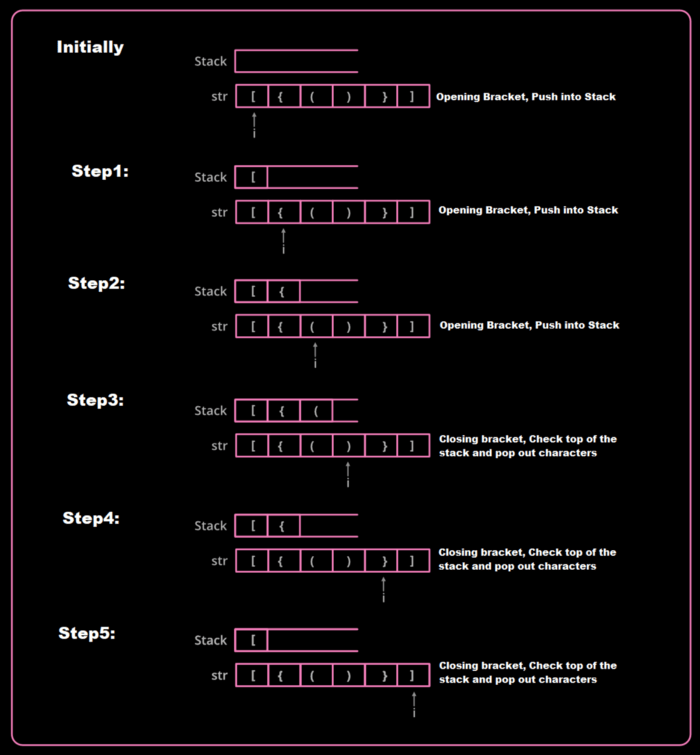Algorithm to check bracket balance using stack data file structure | Image by Author

Now let’s implement the above-mentioned approach.

// Easy Java program for Bracket Pairs checking
import java.util.*;
 
public class BracketPairsChecker {
 
    // Method to check if brackets have complete pair or not.
    public static boolean areBracketsPaired(String expr)
    {
        // Using ArrayDeque is faster than using Stack class
        Deque stack
            = new ArrayDeque();
 
        // Traversing the Expression
        for (int i = 0; i < expr.length(); i++)
        {
            char x = expr.charAt(i);
 
            if (x == '(' || x == '[' || x == '{')
            {
                // Push the element in the stack
                stack.push(x);
                continue;
            }
 
            // If current character is not opening bracket, then it must be closing. So stack cannot be empty at this point.
            if (stack.isEmpty()) {
                return false;
            }
            char check;
            switch (x) {
            case ')':
                check = stack.pop();
                if (check == '{' || check == '[')
                    return false;
                break;
 
            case '}':
                check = stack.pop();
                if (check == '(' || check == '[')
                    return false;
                break;
 
            case ']':
                check = stack.pop();
                if (check == '(' || check == '{')
                    return false;
                break;
            }
        }
 
        // Check Empty Stack
        return (stack.isEmpty());
    }
 
    // Main method to check the code.
    public static void main(String[] args)
    {
        String expr = "[({})]";
        // String expr = "[(){]";
 
        // Function call
        if (areBracketsPaired(expr))
            System.out.println("Paired");
        else
            System.out.println("Not Paired");
    }
}

Output: Paired

Time Complexity: O(n)

Auxiliary Space: O(n) for the stack.

#Easy python3 program to check whether brackets are paired or not.
def areBracketsPaired(expr):
    stack = []
 
    # Traversing the Expression
    for char in expr:
        if char in ["(", "{", "["]:
 
            # Push the element in the stack
            stack.append(char)
        else:
 
            # IF current character is not opening bracket, then it must be closing.So stack cannot be empty at this point.
            if not stack:
                return False
            current_char = stack.pop()
            if current_char == '(':
                if char != ")":
                    return False
            if current_char == '{':
                if char != "}":
                    return False
            if current_char == '[':
                if char != "]":
                    return False
 
    # Check Empty Stack
    if stack:
        return False
    return True
 
 
# Driver Code
if __name__ == "__main__":
    expr = "[(){]"
 
    # Function call
    if areBracketsPaired(expr):
        print("Paired")
    else:
        print("Not Paired")

Output: Not Paired

Time Complexity: O(n)

Auxiliary Space: O(n) for the stack.

// Easy C# program for checking Brackets parenthesis.
using System;
using System.Collections.Generic;
 
public class BalancedBrackets {
    public class stack {
        public int top = -1;
        public char[] items = new char[100];
 
        public void push(char x)
        {
            if (top == 99)
            {
                Console.WriteLine("Stack full");
            }
            else {
                items[++top] = x;
            }
        }
 
        char pop()
        {
            if (top == -1)
            {
                Console.WriteLine("Underflow error");
                return '';
            }
            else
            {
                char element = items[top];
                top--;
                return element;
            }
        }
 
        Boolean isEmpty()
        {
            return (top == -1) ? true : false;
        }
    }
 
    // Returns true if character1 and character2 are matching left and right brackets
    static Boolean isMatchingPair(char character1,
                                  char character2)
    {
        if (character1 == '(' && character2 == ')')
            return true;
        else if (character1 == '{' && character2 == '}')
            return true;
        else if (character1 == '[' && character2 == ']')
            return true;
        else
            return false;
    }
 
    // Return true if expression has balanced Brackets
    static Boolean areBracketsBalanced(char[] exp)
    {
        // Declare an empty character stack */
        Stack st = new Stack();
 
        // Traverse the given expression to check matching brackets
        for (int i = 0; i < exp.Length; i++)
        {
            // If the exp[i] is a starting bracket then push it
            if (exp[i] == '{' || exp[i] == '('
                || exp[i] == '[')
                st.Push(exp[i]);
 
            //  If exp[i] is an ending bracket then pop from stack and check if the popped bracket is a matching pair
            if (exp[i] == '}' || exp[i] == ')'
                || exp[i] == ']') {
 
                // If we see an ending bracket without a pair then return false
                if (st.Count == 0)
                {
                    return false;
                }
 
                // Pop the top element from stack, if it is not a pair brackets of character then there is a mismatch. This happens for expressions like {(})
                else if (!isMatchingPair(st.Pop(),
                                         exp[i])) {
                    return false;
                }
            }
        }
 
        // If there is something left in expression then there is a starting bracket without a closing bracket
 
        if (st.Count == 0)
            return true; // balanced
        else
        {
            // not balanced
            return false;
        }
    }
 
    public static void Main(String[] args)
    {
        char[] exp = { '[', '(', '{', '}', ')', ']' };
 
        // Function call
        if (areBracketsPaired(exp))
            Console.WriteLine("Paired");
        else
            Console.WriteLine("Not Paired");
    }
}

Output: Paired

Time Complexity: O(n)

Auxiliary Space: O(n) for the stack.

#include 
#include 
#define bool int
 
// structure of a stack node
struct sNode {
    char data;
    struct sNode* next;
};
 
// Function to push an item to stack
void push(struct sNode** top_ref, int new_data);
 
// Function to pop an item from stack
int pop(struct sNode** top_ref);
 
// Returns 1 if character1 and character2 are matching left
// and right Brackets
bool isMatchingPair(char character1, char character2)
{
    if (character1 == '(' && character2 == ')')
        return 1;
    else if (character1 == '{' && character2 == '}')
        return 1;
    else if (character1 == '[' && character2 == ']')
        return 1;
    else
        return 0;
}
 
// Return 1 if expression has balanced Brackets
bool areBracketsPaired(char exp[])
{
    int i = 0;
 
    // Declare an empty character stack
    struct sNode* stack = NULL;
 
    // Traverse the given expression to check matching
    // brackets
    while (exp[i])
    {
        // If the exp[i] is a starting bracket then push
        // it
        if (exp[i] == '{' || exp[i] == '(' || exp[i] == '[')
            push(&stack, exp[i]);
 
        // If exp[i] is an ending bracket then pop from
        // stack and check if the popped bracket is a
        // matching pair*/
        if (exp[i] == '}' || exp[i] == ')'
            || exp[i] == ']') {
 
            // If we see an ending bracket without a pair
            // then return false
            if (stack == NULL)
                return 0;
 
            // Pop the top element from stack, if it is not
            // a pair bracket of character then there is a
            // mismatch.
            // his happens for expressions like {(})
            else if (!isMatchingPair(pop(&stack), exp[i]))
                return 0;
        }
        i++;
    }
 
    // If there is something left in expression then there
    // is a starting bracket without a closing
    // bracket
    if (stack == NULL)
        return 1; // balanced
    else
        return 0; // not balanced
}
 
// Driver code
int main()
{
    char exp[100] = "[({})]";
 
    // Function call
    if (areBracketsPaired(exp))
        printf("Paired n");
    else
        printf("Not Paired n");
    return 0;
}
 
// Function to push an item to stack
void push(struct sNode** top_ref, int new_data)
{
    // allocate node
    struct sNode* new_node
        = (struct sNode*)malloc(sizeof(struct sNode));
 
    if (new_node == NULL) {
        printf("Oh No! n");
        getchar();
        exit(0);
    }
 
    // put in the data
    new_node->data = new_data;
 
    // link the old list off the new node
    new_node->next = (*top_ref);
 
    // move the head to point to the new node
    (*top_ref) = new_node;
}
 
// Function to pop an item from stack
int pop(struct sNode** top_ref)
{
    char res;
    struct sNode* top;
 
    // If stack is empty then error
    if (*top_ref == NULL) {
        printf("Oh No n");
        getchar();
        exit(0);
    }
    else {
        top = *top_ref;
        res = top->data;
        *top_ref = top->next;
        free(top);
        return res;
    }
}

Output: Paired

Time Complexity: O(n)

Auxiliary Space: O(n) for the stack.

Hope this article must be helpful for you. If you find joy in what I am doing please give some claps, do some comments and follow me for more upcoming knowledgeable articles.

Read the below articles also: [HIGHLY RECOMMENDED]

1) When to use Interface and Abstract class

2) Top 45+ Collections Java Interview questions

3) How HashMap Works Internally?

4) How HashSet Works Internally?